

SECTION B
[40 marks]
Answer all the questions in this section.
All questions carry equal marks.
(1) A landlord received a total rent of \$240,000.00 in a year. An income tax of 12.5% and a property tax of 20% were paid to the commissioner of income tax. An amount of \$12,000.00 was spent on repairs and the remaining amount was saved. What percentage of the total rent was saved?
[5 marks]
(2) (a) Two functions \( f \) and \( g \) are defined by \( f(x) \rightarrow \frac{x - 1}{2} \) and \( g(x) \rightarrow 3x + 1 \).
(i) Evaluate \( f\left(-\frac{1}{2}\right) + 1 \).
(ii) Solve \( f(x) = g(-2) \).
[5 marks]
(2) (b) The gradient of a line which passes through the point \( (-2, 3) \) is \( \frac{1}{3} \). Find the equation of the line.
[4 marks]
(3) (a) The angle of a sector of a circle of radius \( 7 \, \text{cm} \) is \( 108^\circ \). Calculate the perimeter of the sector. [Take \( \pi = \frac{22}{7} \).]
[5 marks]
(3) (b) Given that \( \frac{4}{\sqrt{3}} \cos(2\theta - 14^\circ) - 2 = 0 \), where \( 0^\circ \leq \theta \leq 90^\circ \), find the value of \( \theta \).
[5 marks]
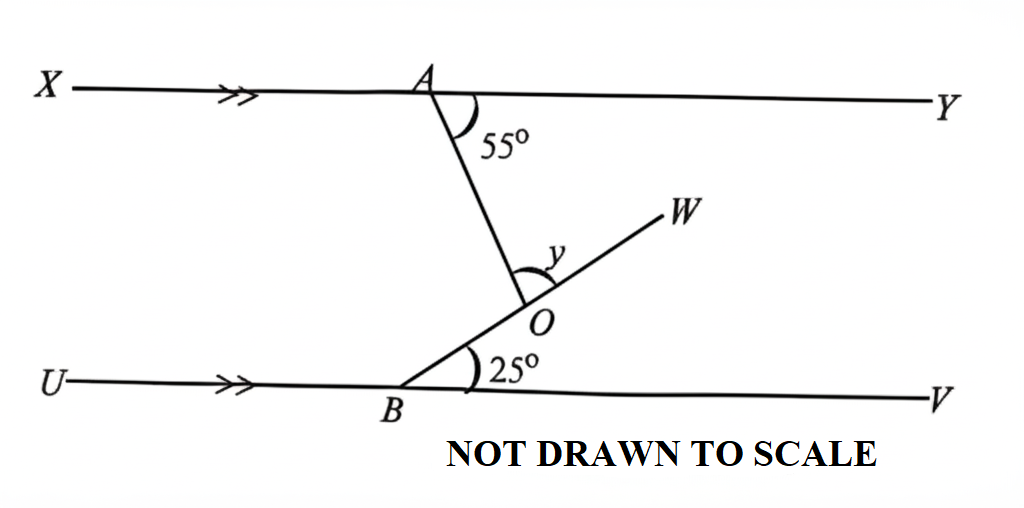
In the diagram, \( \overline{XY} \parallel \overline{UV} \), \( \angle OAY = 55^\circ \) and \( \angle VBW = 25^\circ \). Find the value of the angle marked \( y \).
[5 marks]
(4) (b) Given that \( \log (x^2 + 3) = 2 \log (x + 1) \), find the value of \( x \).
[5 marks]
(5) A number is chosen at random from a set of positive integers, \( P = \{ x : 5 \leq x \leq 24 \} \). Find the probability that the number is:
(a) even or prime;
(b) a perfect square or a multiple of 6.
[10 marks]
SECTION B
[60 marks]
Answer five questions only from this section.
All questions carry equal marks.
(6) Mr. Akoto shared \$8,450.00 amongst John, Anne, and Lillian such that Anne’s share is one-third of Lillian’s share and the ratio of John’s share to Lillian’s share is 2:5. Find:
(a) Anne’s share;
(b) John’s share;
(c) The difference between Lillian and Anne’s shares.
[15 marks]
(7) The data represents the ordered marks scored by 10 students in a test:
10, \( (3x - 1) \), 14, \( (4x - 6) \), 15, \( (x^2 - 8) \), 19, 29, \( (3x + 4) \), and \( 4x \).
(a) Given that the median mark is 16, find the:
(i) value of \( x \);
(ii) mean mark.
(b) If the pass mark for the test is 15, find the percentage of the students who failed.
[15 marks]
(8) A water tank in the form of a cuboid has dimensions \( (x + 1) \, \text{m} \), \( (2x - 3) \, \text{m} \), and 240 cm.
If 67,200 litres of water in the tank is two-thirds of the tank’s capacity, find the value of \( x \).
[7 marks]
(9) A car Y travels due north at a speed of 96 km/h for 30 minutes and another car X travels due east from the same point at 108 km/h for 20 minutes.
(a) Illustrate the information in a diagram.
(b) Find the distance between the two cars.
(c) Find the bearing of car X from Y at that instance.
(10) A bag contains Mathematics, Science and English textbooks, all of the same size and weight. The ratio of the number of Mathematics books to the Science books is 2:3. The number of English books is 1 less than the number of Science books. If the probability of selecting at random an English book is one-third, find the:
(a) Number of each type of book.
(b) Total number of books in the bag.
(11) (a) The ratio of the number of boys to the number of girls in a school of 720 students is 4 : 5. If 26 new girls are admitted into the school, find the number of new boys that must be admitted so that the ratio of the number of boys to the number of girls will be 5 : 6.
[5 marks]
(11) (b) A man spent \( \frac{3}{7} \) of his income on food, \( \frac{1}{4} \) of the remaining income on transport, and \( \frac{1}{3} \) of what still remained on miscellaneous. If the amount left as savings was Le 9,000.00, how much was his income?
[5 marks]
(12) (a) If the distance between two points \( P(-2, m) \) and \( Q(m, 8) \) is \( 5 \sqrt{10} \) units, find the value(s) of \( m \).
[5 marks]
(12) (b) Given that \( 2x^2 - 16x + p = 2(x + q)^2 \) where \( p \) and \( q \) are integers, find the values of \( p \) and \( q \).
[5 marks]

In the diagram, O is the centre of the circle UVWXZ and \( \angle VOX = 120^\circ \). Find:
(i) \( \angle VUX \);
(ii) \( \angle ZYX \);
[5 marks]
(13) (b) Mrs. Abudu is four times as old as her son Kumi. The sum of their ages 5 years ago was 25. At what age did Mrs. Abudu give birth to Kumi?
[5 marks]